IMAGE ENCRYPTION
Abstract
The main aim of this project is to encrypt an image based on Arnold transform with quantum chaotic keys using matlab. The security of digital images is very important and is a major concern as the usage of the internet is rapidly increasing. Henon chaotic map, Arnold transform, Chen’s hyper chaotic system, two-dimensional cellular automata based method are few algorithms which were used to encrypt an image. In this project we are going to use Arnold transform to encrypt an image. Arnold method is a classical method and has a disadvantage that it will only work for NxN matrices, so as to deal with this problem a pseudo-random system is applied to generate random sequences to encrypt colour images. Chaotics are highly efficient, they are sensitive to initial parameters and conditions, they are highly ergodic and have mixing properties. To encrypt the colour images, in this project we use Herein, a quantum chaotic system to generate pseudo-random sequences. Image encryption has many applications as it can be used to keep our images private over the internet. It is widely used in military based operations, health care sectors, corporate worlds and in multimedia systems. Encryption shields personal information, touchy data, and strengthens the safety of conversation among customer apps and servers.

Code Description & Execution
Algorithm Description
- Arnold transform does not adapt to image NxN, it is necessary to transform image WxH into NxN.
to do so, we use the following equation :
N = max([W, H]
…..where N is the maximum value between ‘W’ and ‘H’.
- If W=H , N=W=H (it simply means that the image is in a square) then the image will not be amplified. else the image will be amplified.
- Random numbers are generated by the random function to fill the increased part of image pixel values. With this the randomness of the cryptosystem is increased and the real width and the height of the image will remain unknown until decryption. Now the image P of WxH has become the image of NxN.
- The matrix P(image) with red, green, and blue components is converted into three matrices R, G, and B. Then the permutation process is applied to R,G and B matrices.
Permutation process for matrix R :- In this process pseudo random key streams are generated to change the colour image(P) pixels.
Then this process is repeated to the G and B matrix and the process should be iterated n times to get the cipher image. the R,G and B matrices will now become R0,G0 and B0
Diffusion process :- to generate the initial condition set the L=NxN. then iterate the following equation m+L times :
x 0 n+1 = (1 − ε)ϕ(x 0 n+1) + εϕ(y 0 n+1)
y 0 n+1 = (1 − ε)ϕ(y 0 n+1) + εϕ(z 0 n+1)
z 0 n+1 = (1 − ε)ϕ(z 0 n+1) + εϕ(x 0 n+1)
- transform R,G and B matrices into vectors.
- apply encryption transformation.
equation of encryption transformation :-
Cri = ((floor(Rm+i × W × H × k6 × k7 × k9 × k10 × k12 × k13)mod 256) ⊕ ri Cgi = ((floor(Gm+i × W × H × k5 × k7 × k8 × k10 × k11 × k13)mod 256) ⊕ gi Cbi = ((floor(Bm+i × W × H × k5 × k6 × k8 × k9 × k11 × k12)mod 256) ⊕ bi set initial values i = 1.Set i = i+1 and then iterating this step until i ≤ L we can get three matrices Cr, Cg and Cb.
DECRYPTION ALGORITHM :
The decryption process is similar to the encryption process, but it is carried out in the reverse order.
- Step 1: Apply the external 128-bit secret key used in the encryption process.
- Step 2: Substituting the initial condition (x 0 0, y 0 0, z 0 0) and iterating the below equation m+L times, discarding the former m values to avoid harmful effects, where m = 13.
the equation is :-
x 0 n+1 = (1 − ε)ϕ(x 0 n+1) + εϕ(y 0 n+1)
y 0 n+1 = (1 − ε)ϕ(y 0 n+1) + εϕ(z 0 n+1)
z 0 n+1 = (1 − ε)ϕ(z 0 n+1) + εϕ(x 0 n+1)
- Step 3: Sorting these values X = {x m+1, x m+2, … , x m+L}, Y = {ym+1, ym+2, … , ym+L} and Z= {z m+1, z m+2, … , z m+L}. Setting i = 1 and iterating the encryption transformation equation until i = L we can get three vectors −→ C 0 r , −→ C 0 g and −→ C 0 b .
the equation is :-
- Step 4: We convert these vectors into three matrices R0 r, G0 g and B 0 b whose size are all N ×N . Substituting parameters ai , bi and the initial condition (kµi , kνi) T (i = 1, 2, 3), and then using the encryption algorithm equation we get R0 , G0 , B 0 of the image, According to the width W and the height H of the plain-image we tailor R0 , G0 , B 0 and get plain values of R, G and B. In this way the encryption process finished.
Code Description
Code Description:
There are three main codes for execution of project they are:
- m
- m
- m
Note:
- We don’t need to run these codes “m and test.m” file due to it being a “function which will be included in the main code.
Note: MATLAB file or codes are saved in .m and .mat format
Steps to Execute the Code
1.Download the zip file and unzip it, you will find all required files
2.Open MATLAB and click on the ‘browse for folder’ icon as shown below
3. A popup window appears from which we can select the folder
4. Add all .m files in that folder as shown below.
5. Run module2.m file.
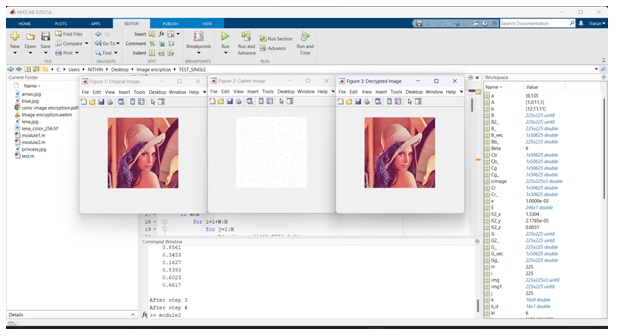
Result
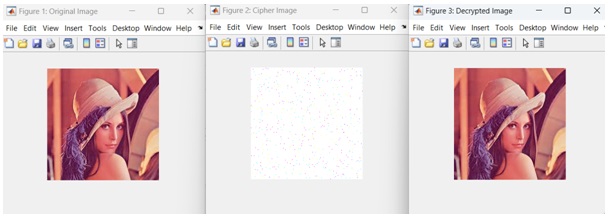
Issues Faced
- Must install the current version of MATLAB and add on should be added.
- Download the required addons.
